The ‘1000 Mathematical Olympiad Problems’ PDF offers a comprehensive collection of challenging exercises designed to enhance problem-solving abilities and prepare students for international competitions effectively.
1.1 Overview of Mathematical Olympiads
Mathematical Olympiads are prestigious international and regional competitions testing advanced problem-solving skills in algebra, geometry, and number theory. The International Mathematical Olympiad (IMO) is the premier event, attracting top students worldwide. These competitions require deep conceptual understanding and creativity. The ‘1000 Mathematical Olympiad Problems’ PDF serves as a valuable resource, offering diverse challenges that mirror Olympiad-style questions, helping participants prepare for such high-level mathematical competitions effectively.
1.2 Importance of Practicing Olympiad Problems
Practicing Olympiad problems is crucial for developing advanced problem-solving skills and mathematical reasoning. It enhances logical thinking, creativity, and the ability to approach complex challenges systematically. Regular practice with resources like the ‘1000 Mathematical Olympiad Problems’ PDF helps build confidence, improves time management, and familiarizes students with diverse problem types. This preparation is essential for excelling in international competitions and fostering a deep understanding of mathematical concepts.

Key Features of the “1000 Mathematical Olympiad Problems” PDF
The PDF offers a diverse collection of 1000 carefully curated problems, covering algebra, geometry, number theory, and combinatorics. It provides a structured format for systematic practice, catering to all skill levels.
2.1 Structure and Organization of the PDF
The ‘1000 Mathematical Olympiad Problems’ PDF is meticulously organized, categorizing problems by difficulty and topic. It covers algebra, geometry, number theory, and combinatorics, with clear sections for each category. The document includes problem statements, hints, and detailed solutions, making it a valuable resource for systematic practice. An index and cross-references enhance navigation, allowing users to focus on specific areas or progress through levels of difficulty seamlessly.
2.2 Topics Covered in the Problems
The PDF encompasses a wide range of mathematical disciplines, including algebra, number theory, geometry, trigonometry, and combinatorics. It features problems on equations, inequalities, divisibility, prime numbers, and advanced geometric proofs. Additionally, it covers probability, combinatorial strategies, and complex problem-solving techniques. The diverse topics ensure comprehensive preparation for various Olympiad challenges, making it an invaluable resource for students aiming to excel in international mathematical competitions.

Benefits of Using the “1000 Mathematical Olympiad Problems” PDF
Enhances problem-solving skills and provides comprehensive preparation for international mathematical competitions, offering a structured approach to mastering various mathematical concepts and techniques essential for Olympiad success.
3.1 Enhancing Problem-Solving Skills
The ‘1000 Mathematical Olympiad Problems’ PDF equips students with advanced techniques to tackle complex problems, fostering critical thinking and adaptability. By engaging with diverse problem types, learners refine their analytical abilities, master theoretical concepts, and develop innovative solutions. This resource is particularly effective for improving algebraic manipulation, geometric reasoning, and combinatorial logic, ensuring a strong foundation for competitive mathematics and real-world problem-solving challenges.
3.2 Preparing for International Competitions
The ‘1000 Mathematical Olympiad Problems’ PDF is an invaluable resource for students aiming to excel in international competitions like the IMO. It provides a diverse range of challenging problems that align with competition standards, covering key areas such as algebra, geometry, and combinatorics. The structured format allows learners to practice strategically, building both speed and accuracy. Regular practice with these problems sharpens problem-solving strategies and prepares students to tackle the rigorous demands of global mathematical competitions effectively.
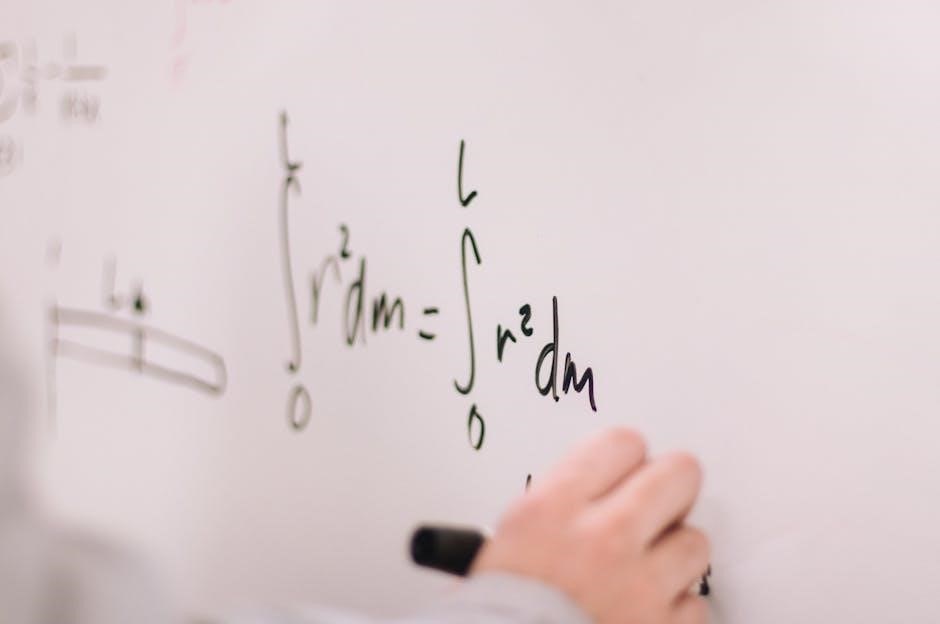
Common Mathematical Concepts in Olympiad Problems
Olympiad problems often involve core concepts like algebra, geometry, number theory, combinatorics, and probability, requiring deep understanding and creative application of mathematical principles to solve effectively.
4.1 Algebra and Number Theory
Algebra and number theory form the backbone of many Olympiad problems, focusing on techniques like factorization, modular arithmetic, and Diophantine equations. These problems often require innovative applications of theorems and properties to find integer solutions or prove statements. The ‘1000 Mathematical Olympiad Problems’ PDF includes a wide range of exercises that test proficiency in algebraic manipulations and number-theoretic insights, essential for mastering higher-level mathematical competitions and developing robust problem-solving strategies.
4.2 Geometry and Trigonometry
Geometry and trigonometry are central to Olympiad problems, often involving advanced spatial reasoning and logical thinking. The ‘1000 Mathematical Olympiad Problems’ PDF includes exercises on triangle properties, circle theorems, and trigonometric identities. Classic problems, such as those involving cyclic quadrilaterals or angle optimizations, are frequently featured. These challenges demand precise calculations and creative approaches, making them ideal for honing geometrical problem-solving skills and preparing for high-level competitions.
4.3 Combinatorics and Probability
Combinatorics and probability problems in the PDF focus on logical reasoning and strategic thinking. Exercises include permutations, combinations, and probability distributions, often requiring innovative approaches. Classic problems involve counting principles, probabilistic events, and optimal strategies. These challenges enhance analytical skills and prepare students for complex combinatorial scenarios in international competitions, fostering a deep understanding of probability theory and its applications in mathematics.

Advanced Techniques for Solving Olympiad Problems
The PDF introduces specialized theorems, lemmas, and geometrical strategies to tackle complex problems, providing a comprehensive toolkit for mastering advanced mathematical techniques and building problem-solving expertise.
5.1 Specialized Theorems and Lemmas
The ‘1000 Mathematical Olympiad Problems’ PDF includes a wide range of specialized theorems and lemmas essential for solving advanced problems. These mathematical tools, such as the Pigeonhole Principle, Geometric Transformations, and Number Theory concepts, are explained with clear examples. The resource emphasizes how these theorems can be applied to tackle complex Olympiad questions, providing students with a solid foundation to approach challenging problems confidently and strategically.
5.2 Geometrical Problem-Solving Strategies
The PDF introduces advanced geometrical strategies, such as exploiting symmetry, applying coordinate geometry, and using trigonometric identities. It emphasizes techniques like inversion, reflection, and vector analysis to simplify complex problems. Additionally, it highlights the importance of diagrammatic reasoning and transformational geometry. These methods are illustrated with detailed examples, enabling students to approach Olympiad geometry problems with confidence and creativity, ensuring a deep understanding of spatial relationships and problem-solving techniques.

AI and Technology in Solving Mathematical Olympiad Problems
AI systems like AlphaGeometry 2 and AlphaProof are revolutionizing Olympiad problem-solving by tackling complex geometry and mathematical reasoning challenges, achieving silver-medal standards in international competitions.
6.1 AI Systems like AlphaGeometry 2
AI systems such as AlphaGeometry 2 are advancing mathematical problem-solving by automating geometrical reasoning and diagram generation. These tools enhance problem-solving efficiency and provide insights, aiding Olympiad training and fostering innovation in mathematics education.
6.2 Impact of AI on Olympiad Training
AI systems like AlphaGeometry 2 are revolutionizing Olympiad training by solving complex problems and generating detailed solutions. These tools provide personalized learning experiences, enhance problem-solving strategies, and offer real-time feedback. AI’s ability to tackle high-level problems accelerates skill development, making it an invaluable resource for aspiring competitors. This technological advancement is reshaping how students prepare for international competitions, fostering innovation and efficiency in mathematical education.

Selecting the Right Problems for Practice
Selecting problems by difficulty and aligning them with competition goals ensures effective practice. The PDF offers a structured approach to cater to diverse skill levels and objectives.
7.1 Categorizing Problems by Difficulty
Categorizing problems by difficulty helps students progress systematically. The PDF organizes problems from basic to advanced, covering algebra, geometry, and combinatorics. This structure allows learners to master foundational concepts before tackling complex challenges. Resources like “Mathematical Olympiad Treasures” and “A First Step to Mathematical Olympiad Problems” also emphasize this approach. By focusing on categorized practice, students can identify and improve weak areas, ensuring a well-rounded preparation for competitions.
7.2 Aligning Problems with Competition Goals
Aligning problems with competition goals ensures focused preparation. The PDF includes exercises mirroring International Mathematical Olympiad (IMO) challenges, covering algebra, geometry, and combinatorics. Past problems and solutions, like those from “Mathematical Olympiad Treasures,” aid in targeted practice. By studying these, students can identify competition patterns and refine their strategies, ensuring they are well-prepared for the specific demands of international and regional competitions, ultimately enhancing their performance and confidence.

Examples of Classic Olympiad Problems
The PDF includes classic problems in algebra, geometry, and number theory, such as solving equations, proving inequalities, and geometric constructions, mirroring past IMO challenges.
8.1 Geometry and Trigonometry Examples
The PDF features diverse geometry problems, including point-circle-triangle configurations, trigonometric identities, and spatial reasoning exercises. These examples, inspired by past IMO challenges, test contestants’ understanding of angles, distances, and shapes. Classic problems involve proving congruencies, calculating areas, and applying theorems like Pythagoras and Ptolemy. Trigonometric questions explore sine, cosine, and tangent functions, often in dynamic settings. These exercises refine spatial reasoning and logical thinking, essential for advanced geometrical problem-solving.
8.2 Number Theory and Algebra Examples
The PDF includes a wide range of number theory and algebra problems, such as solving Diophantine equations, exploring modular arithmetic, and manipulating algebraic expressions. Classic examples involve finding all positive integers ( n ) that satisfy given conditions or proving properties of sequences. These exercises challenge participants to apply number theory concepts like divisibility and prime factorization, while algebra problems focus on solving systems of equations and optimizing expressions. They are designed to refine critical thinking and logical reasoning skills.

Resources for Further Study
Recommended books include “A First Step to Mathematical Olympiad Problems” and online platforms like AoPS and Mathematical Olympiad Treasures for additional practice and strategies.
9.1 Recommended Books and PDFs
Essential resources include “A First Step to Mathematical Olympiad Problems” and “Mathematical Olympiad Treasures,” offering diverse problem sets and solutions. The “Eisatopon Math AI Challenges” and “Asian Pacific Mathematics Olympiad (APMO) Problems and Solutions” provide extensive practice materials. Additionally, “Mathematical Olympiads 1995-1996: Olympiad Problems from Around the World” and “Mathematical Intelligencer” articles are invaluable for advanced preparation. These resources cover algebra, geometry, and combinatorics, ensuring a well-rounded study experience.
9.2 Online Platforms for Olympiad Preparation
Online platforms like AoPS (Art of Problem Solving) and Online Math Club offer extensive resources, including problem sets, solutions, and forums. Google DeepMind’s AlphaGeometry 2 provides AI-driven solutions for geometry problems. These platforms, along with Eisatopon Math AI Challenges, enable students to practice and refine their skills dynamically. They also offer interactive tools and community support, making Olympiad preparation more accessible and engaging for aspiring participants worldwide.

Training Programs and Competitions
Training programs and competitions are essential for honing mathematical skills, with resources like the ‘1000 Mathematical Olympiad Problems’ PDF aiding in structured practice and competition preparation.
10.1 International Mathematical Olympiad (IMO)
The International Mathematical Olympiad (IMO) is the most prestigious global mathematics competition for high school students, held annually since 1959. It features six challenging problems solved over two days, each worth seven points. Recent advancements include AI systems like AlphaGeometry 2 solving four IMO problems, matching silver medal standards. The IMO fosters deep problem-solving skills, logical thinking, and mathematical excellence, preparing students for advanced academic and professional pursuits in mathematics.
10.2 Regional and National Competitions
Regional and national mathematical Olympiads serve as stepping stones for the IMO, offering students valuable competition experience. The ‘1000 Mathematical Olympiad Problems’ PDF is a valuable resource for these competitions, covering a wide range of topics like algebra, geometry, and combinatorics. It helps students adapt to diverse problem styles and difficulty levels, fostering strategic thinking and exam readiness. Regular practice with such materials enhances problem-solving techniques and builds confidence for higher-level competitions.
The ‘1000 Mathematical Olympiad Problems’ PDF is an invaluable resource for mastering Olympiad-level mathematics, fostering problem-solving skills, and building confidence for competitions.
11.1 Final Thoughts on the Importance of Practice
Consistent practice with resources like the ‘1000 Mathematical Olympiad Problems’ PDF is essential for mastering problem-solving skills and analytical thinking. Regular engagement with challenging problems enhances mathematical intuition and prepares students for high-level competitions. By dedicating time to solve diverse problems, learners can refine their strategies and gain confidence in tackling complex mathematical concepts, ultimately fostering long-term success in Olympiad-level mathematics.
11.2 Encouragement for Aspiring Participants
Embrace the challenge of mathematical Olympiad problems with confidence and determination. The ‘1000 Mathematical Olympiad Problems’ PDF serves as a powerful tool to unlock your potential and refine your skills. Start early, stay persistent, and leverage these resources to build a strong foundation. With dedication and the right guidance, aspiring participants can master complex concepts and excel in international competitions, turning their passion for mathematics into a rewarding journey of discovery and achievement.
